Описательная статистика на Python

Для изучения статистики загружаем библиотеки: math, numpy, pandas, statistics, scipy.stats. Посмотрим, каким образом можно рассчитать центральные метрики, средневзвешенное, гармоническое среднее, среднее геометрическое, медиану, моду, дисперсию, среднеквадратичное отклонение, смещение, процентили, диапазон. Программный код для расчёта данных показателей приведён ниже.

#
import math
import statistics
import numpy as np
import scipy.stats
import pandas as pd
print("Исходные данные")
x = [8.0, 1, 2.5, 4, 28.0]
x_with_nan = [8.0, 1, 2.5, math.nan, 4, 28.0]
y, y_with_nan = np.array(x), np.array(x_with_nan)
z, z_with_nan = pd.Series(x), pd.Series(x_with_nan)
print(y)
print(y_with_nan)
print(z)
print(z_with_nan)

# Среднее значение
print("Среднее значение")
mean_=sum(x)/len(x)
print(mean_)
mean_=statistics.mean(x)
print(mean_)
m=np.nanmean(y_with_nan)
print(m)


# Средневзвешенное значение
print("Средневзвешенное значение")
x = [8.0, 1, 2.5, 4, 28.0]
w = [0.1, 0.2, 0.3, 0.25, 0.15]
wmean = sum(w[i] * x[i] for i in range(len(x))) / sum(w)
print(wmean)
wmean = sum(x_ * w_ for (x_, w_) in zip(x, w)) / sum(w)
print(wmean)
# Средневзвешенное значение, использование массивов Numpy и Pandas
x = [8.0, 1, 2.5, 4, 28.0]
y, z, w = np.array(x), pd.Series(x), np.array(w)
wmean = np.average(y, weights=w)
print(wmean)
wmean = np.average(z, weights=w)
print(wmean)

# Гармоническое среднее
print("Гармоническое среднее")
hmean = len(x) / sum(1 / item for item in x)
print(hmean)
hmean==scipy.stats.hmean(y)
print(hmean)

# Среднее геометрическое
print("Среднее геометрическое")
gmean = 1
for item in x:
    gmean *= item
gmean **= 1 / len(x)
print(gmean)

# Медиана
print("Медиана")
n = len(x)
if n % 2:
    median_ = sorted(x)[round(0.5*(n-1))]
else:
    x_ord, index = sorted(x), round(0.5 * n)
    median_ = 0.5 * (x_ord[index-1] + x_ord[index])
print(median_)
print(z.median())
print(z_with_nan.median())

# Медиана
u = [2, 3, 2, 8, 12]
mode_ = max((u.count(item), item) for item in set(u))[1]
print(mode_)


# Дисперсия
print("Дисперсия")
n = len(x)
mean_ = sum(x) / n
var_ = sum((item - mean_)**2 for item in x) / (n - 1)
print(var_)

# Среднеквадратическое отклонение
print("Среднеквадратическое отклонение")
std_ = var_ ** 0.5
print(std_)
std_=np.std(y, ddof=1)
print(std_)

# Смещение
print("Смещение")
y, y_with_nan = np.array(x), np.array(x_with_nan)
print(scipy.stats.skew(y, bias=False))
print(scipy.stats.skew(y_with_nan, bias=False))

# Процентили
print("Процентили")
y = np.array(x)
print(np.percentile(y, 5))
print(np.percentile(y, 95))

# Диапазон
print("Диапазон")
print(np.amax(y) - np.amin(y))
print(np.nanmax(y_with_nan) - np.nanmin(y_with_nan))
print(y.max() - y.min())
print(z.max() - z.min())
print(z_with_nan.max() - z_with_nan.min())

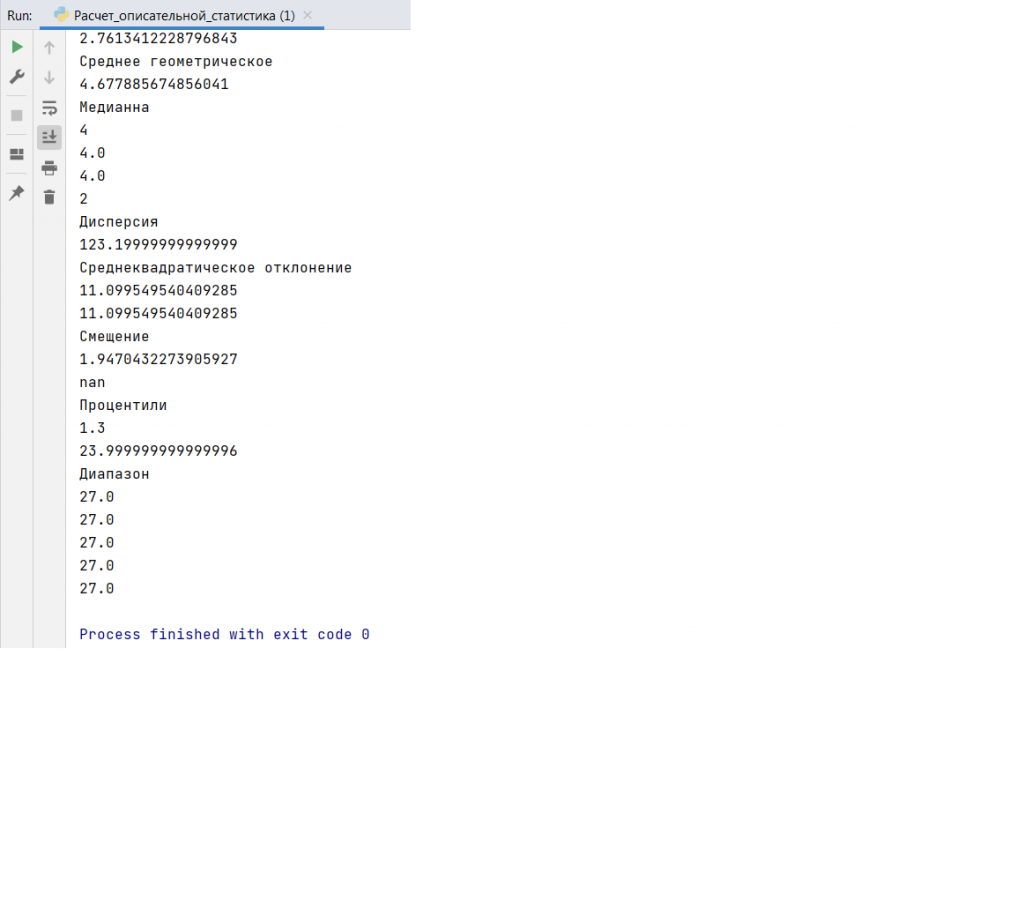
Результат работы программы представлен ниже.