В предыдущей части мы уже начали разбирать описательную статистику, а именно: центральные метрики и метрики оценки вариативности. В этой же части мы будем говорить той же описательной статистики, но уже разберем корреляции между парами данных. Корреляция – это статистическая взаимосвязь между двумя или более случайными величинами. И есть две статистические меры, которые характеризуют корреляцию между наборами данных — ковариация и коэффициент корреляции. Но прежде, чем нам начать с ними работать, необходимо установить и импортировать нужные библиотеки, а именно: math, statistics, numpy, scipy.stats, pandas и matplotlib.pyplot. После этого, мы формируем два списка Python, которые будем использовать для получения соответствующих массивов NumPy и серии Pandas:
x = list(range(-10, 11)) y = [0, 2, 2, 2, 2, 3, 3, 6, 7, 4, 7, 6, 6, 9, 4, 5, 5, 10, 11, 12, 14] x_, y_ = np.array(x), np.array(y) x__, y__ = pd.Series(x_), pd.Series(y_)
Теперь, когда у нас есть исходные данные, можно начать исследовать взаимосвязи между ними.
Ковариации
Выборочная ковариация — это мера, которая количественно определяет силу и направление взаимосвязи между парой переменных:
• Если корреляция положительная, то и ковариация тоже положительная. Более сильное отношение соответствует более высокой ценности ковариации.
• Если корреляция отрицательна, то и ковариация также отрицательна. Более сильное отношение соответствует более низкому (или более высокому абсолютному) значению ковариации.
• Если корреляция слабая, то ковариация близка к нулю.
Процесс расчета ковариации представлен ниже:
#Ковариация
#Расчет ковариации в чистом Python
mean_x, mean_y = sum(x) / n, sum(y) / n
cov_xy = (sum((x[k] - mean_x) * (y[k] - mean_y) for k in range(n))/ (n - 1))
print(f'Расчет ковариации в чистом Python: {cov_xy}')
#Расчет ковариации с помощью NumPy
cov_matrix = np.cov(x_, y_)
print(f'Расчет ковариационной матрицы с помощью NumPy функцией cov(): {cov_matrix}')
print(f'Проверка, что левый элемент ковариационной матрицы — это ковариация x и x или дисперсия x, '
f'а правый элемент — ковариация y и y или дисперсия y: {x_.var(ddof=1)} и {y_.var(ddof=1)}')
cov_xy = cov_matrix[0, 1]
cov_xy2 = cov_matrix[1, 0]
print(f'Проверка, что два других элемента ковариационной матрицы равны '
f'и представляют фактическую ковариацию между x и y: {cov_xy} и {cov_xy2}')
#Расчет ковариации с помощью Pandas
cov_xy = x__.cov(y__)
cov_xy3 = y__.cov(x__)
print(f'Расчет ковариации с помощью Pandas методом .cov(): {cov_xy} и {cov_xy3}')
Первым делом была найдена ковариация в чистом Python, где сначала необходимо найти среднее значение х и у, а затем применить математическую формулу. Но можно применить функцию cov() библиотеки NumPy, которая возвращает ковариационную матрицу, что и было сделано во втором примере. Обратите внимание, cov() имеет необязательные параметры bias (по умолчанию False) и ddof (по умолчанию None). Их значения по умолчанию подходят для получения образца ковариационной матрицы. Верхний левый элемент ковариационной матрицы — это ковариация x и x или дисперсия x. Точно так же нижний правый элемент — y и y или дисперсия y. А два других элемента ковариационной матрицы равны и представляют фактическую ковариацию между x и y. Как проверить и убедиться, что это правда, разобрано в примере. Использовав np.cov() мы получили то же значение ковариации, что и с чистым Python. Помимо этого, можно было использовать метод .cov() библиотеки Pandas, что и было сделано в третьем примере, где для одного объекта Series вызывается .cov() и передает другой объект в качестве первого аргумента.
Коэффициент корреляции
Коэффициент корреляции или коэффициент корреляции Пирсона — произведение, обозначается символом ??. Коэффициент является еще одним показателем корреляции между данными. К нему надо относиться как к стандартизированной ковариации. Вот несколько важных замечаний:
• ? > 0 указывает на положительную корреляцию.
• ? < 0 указывает на отрицательную корреляцию.
• r = 1 является максимально возможным значением ?. Это свидетельство полной линейной зависимости между переменными.
• r = −1 является минимально возможным значением ?. Это свидетельство полного отсутствия линейной зависимости между переменными.
• r ≈ 0 или когда around около нуля, означает, что корреляция между переменными отсутствует.
Процесс расчета коэффициента корреляции представлен ниже:
#Коэффициент корреляции
#Расчет коэффициента корреляции в чистом Python
var_x = sum((item - mean_x)**2 for item in x) / (n - 1)
var_y = sum((item - mean_y)**2 for item in y) / (n - 1)
std_x, std_y = var_x ** 0.5, var_y ** 0.5
r = cov_xy / (std_x * std_y)
print(f'Расчет коэффициента корреляции в чистом Python: {r}')
#Расчет коэффициента корреляции с помощью scipy.stats
r, p = scipy.stats.pearsonr(x_, y_)
print(f'Расчет коэффициента корреляции и p-value, используя функцию pearsonr() в scipy.stats: {r} и {p} ')
scipy.stats.linregress(x_, y_)
print(f'Расчет коэффициента корреляции с помощью scipy.stats.linregress(): {scipy.stats.linregress(x_, y_)}')
result = scipy.stats.linregress(x_, y_)
r = result.rvalue
print(f'Получение доступа к определенным значениям из результата linregress(), включая коэффициент корреляции, используя точечную запись: {r}')
#Расчет коэффициента корреляции с помощью Pandas
r = x__.corr(y__)
r1 = y__.corr(x__)
print(f'Расчет коэффициента корреляции методом .corr() библиотеки Pandas: {r} и {r1}')
В первом примере показано, как рассчитать это коэффициент в чистом Python. Для этого нам понадобятся средние значения (mean_x и mean_y) и стандартные отклонения (std_x, std_y) для наборов данных x и y, а также их ковариация cov_xy. Далее, этот коэффициент и значение p-value (значение, показывающее принимается или отклоняется гипотеза) были рассчитан с помощью функцию pearsonr() в scipy.stats. Первое значение - это коэффициент корреляции между x_ и x_. Второй элемент — это коэффициент корреляции между y_ и y_. Их значения равны 1,0. В третьем примере коэффициент корреляции был найдем с помощью scipy.stats.linregress(). linregress() принимает x_ и y_, вычисляет линейную регрессию и возвращает результаты — наклон и точка пересечения определяют уравнение прямой регрессии, а rvalue — коэффициент корреляции. Чтобы получить доступ к определенным значениям из результата linregress(), включая коэффициент корреляции, необходимо использовать точечную запись, что показано в примере. И в четвертом примере был использован метод .corr() библиотеки Pandas, который вызывается для одного объекта Series и передает другой объект в качестве первого аргумента.
Работа с 2D данными
Axis
В статистике очень часто работают с 2D данными. NumPy и SciPy предоставляют комплексные средства для работы с ними, а Pandas имеет специальный класс DataFrame для обработки 2D данных. И прежде, чем нам работать с ними, их необходимо создать:
#Работа с данными 2D (таблицы) #Axis #Создание 2D массива с помощью Numpy a = np.array(2, 3, 1],[4, 9, 2], [8, 27, 4], [16, 1, 1], [2, 3, 1એ) print(f'Вывод, созданного с помощью Numpy, 2D массива: {a}')
Теперь у нас есть набор 2D данных, который мы будем использовать в этом разделе. Можно применять к нему статистические функции и методы Python так же, как к данным 1D, используя или не используя при этом необязательный параметр axis, то есть ось. Ось может принимать любое из следующих значений:
• axis = None — расчет статистики по всем данным в массиве, как в приведенном выше примере. Такое поведение часто используется по умолчанию в NumPy.
• axis = 0 — расчет статистики для каждого столбца массива. Такое поведение часто используется по умолчанию для статистических функций SciPy.
• axis = 1 — расчет статистики для каждой строки массива.
Внизу представлен код, в котором я попробовал использовать к нашему 2D данным статистические функции и методы Python, как с параметром axis, так и без:
#Использование статистических функций и методов Python к 2d массиву с необязательным параметров axis
np.mean(a, axis=0)
a.mean(axis=1)
print(f'Вывод среднего значения 2D массива методом NumPy на оси = 0 и на оси = 1 соответствнно: {np.mean(a, axis=0)} и {a.mean(axis=1)}')
np.median(a, axis=0)
np.median(a, axis=1)
print(f'Вывод медианы 2D массива методом NumPy на оси = 0 и на оси = 1 соответствнно: {np.median(a, axis=0)} и {np.median(a, axis=1)}')
scipy.stats.gmean(a) # Default: axis=0
print(f'Вывод среднего геометрического значения 2D массива функцией SciPy на оси = 0 : {scipy.stats.gmean(a)}')
scipy.stats.gmean(a, axis=None)
print(f'Вывод среднего геометрического значения для всего 2D массива функцией SciPy: {scipy.stats.gmean(a, axis=None)}')
DataFrames
Класс DataFrame является одним из основных типов данных Pandas. С ним очень удобно работать, потому что в нем есть метки для строк и столбцов. Сам код представлен внизу:
#DataFrames
row_names = ['first', 'second', 'third', 'fourth', 'fifth']
col_names = ['A', 'B', 'C']
df = pd.DataFrame(a, index=row_names, columns=col_names)
print(f'Вывод класса DataFrame с ранее созданным 2d массивом: {df}')
df.mean()
df.var()
print(f'Вывод среднего значения и несмещенной дисперсии для всего класса DataFrame с ранее созданным 2d массивом: {df.mean()} и {df.var()}')
df.mean(axis=1)
print(f'Вывод среднего значения класса DataFrame с ранее созданным 2d массивом по оси = 1: {df.mean(axis=1)}')
df['A']
print(f'Пример изоляции класса DataFrame с ранее созданным 2d массивом по столбцу A: {df["A"]}')
df['A'].mean()
print(f'Пример расчета среднего значения класса DataFrame с ранее созданным 2d массивом по столбцу A: {df["A"].mean()}')
Первым делом был создан DataFrame использовав при этом массив a. На практике имена столбцов имеют значение и должны быть описательными. Имена строк иногда указываются автоматически как 0, 1 и т. Д. Вы можете указать их явно с помощью параметра index, хотя вы можете свободно опускать index, если хотите. Методы DataFrame очень похожи на методы Series, хотя их поведение отличается. Если вы вызываете методы статистики Python без аргументов, то DataFrame будет возвращать результаты для каждого столбца. Если же вы хотите получить результаты для каждой строки, просто укажите параметр axis = 1. Также можно изолировать каждый столбец DataFrame и применять к нему соответствующие методы. Процесс применения статистических методов и функций Python к DataFrame представлен в примере.
Визуализация данных
В дополнение к численному описанию, такому как среднее, медиана или дисперсия, можно использовать визуальные методы для представления, описания и обобщения данных. В этом разделе вы узнаете, как представить свои данные визуально, используя библиотеку matplotlib.pyplot, которая у нас уже установлена и импортирована. matplotlib.pyplot — очень удобная и широко используемая библиотека, хотя это не единственная библиотека Python, доступная для этой цели.
Box Plots
Ящик с усами является отличным инструментом для визуального представления описательной статистики данного набора данных. Он может показывать диапазон, межквартильный диапазон, медиану, моду, выбросы и все квартили. Сам код:
#Визуализация данных
#Box Plots
np.random.seed(seed=0)
x = np.random.randn(1000)
y = np.random.randn(100)
z = np.random.randn(10)
fig, ax = plt.subplots()
ax.boxplot((x, y, z), vert=False, showmeans=True, meanline=True,
labels=('x', 'y', 'z'), patch_artist=True,
medianprops={'linewidth': 2, 'color': 'purple'},
meanprops={'linewidth': 2, 'color': 'red'})
plt.show()
Первый оператор инициализирует генератора случайных чисел NumPy с помощью seed(). Поэтому при каждом запуске скрипта могут получаться одинаковые результаты. Не нужно устанавливать начальное значение и, если его не указывать, то каждый раз будут получаться разные результаты. Другие операторы создают три массива NumPy с нормально распределенными псевдослучайными числами. x относится к массиву с 1000 элементами, y имеет 100, а z содержит 10 элементов. Параметры .boxplot():
• х ваши данные.
• vert устанавливает горизонтальную ориентацию графика, когда False. Ориентация по умолчанию - вертикальная.
• showmeans показывает среднее значение ваших данных, когда True.
• meanline представляет среднее в виде линии, когда истина. Представлением по умолчанию является точка.
• labels: метки ваших данных.
• patch_artist определяет, как рисовать график.
• medianprops обозначает свойства линии, представляющей медиану.
• meanprops указывает свойства линии или точки, представляющей среднее значение.
Есть и другие параметры, но их анализ выходит за рамки данного руководства. Вы можете увидеть три сюжета. Каждый из них соответствует одному набору данных (x, y или z) и показывает следующее:
• Среднее значение — это красная пунктирная линия.
• Медиана — это фиолетовая линия.
• Первый квартиль — левый край синего прямоугольника.
• Третий квартиль — это правый край синего прямоугольника.
• Межквартильный диапазон — это длина синего прямоугольника.
• Диапазон — всё слева направо.
• Выбросы — точки слева и справа.
Сюжетная диаграмма может показывать столько информации на одном рисунке!
Результат:

Гистограммы
Гистограмма особенно полезна, когда в наборе данных содержится большое количество уникальных значений. Гистограмма делит значения из отсортированного набора данных на интервалы, также называемые ячейками. Часто все лотки имеют одинаковую ширину, но это не обязательно так. Значения нижней и верхней границ ячейки называются ребрами ячейки. Частота представляет собой одно значение, которое соответствует каждому бину. Это количество элементов набора данных со значениями между краями корзины. По договоренности, все корзины, кроме самой правой, наполовину открыты. Они включают значения, равные нижним границам, но исключают значения, равные верхним границам. Крайняя правая корзина закрыта, так как включает обе границы. Если вы разделите набор данных с ребрами 0, 5, 10 и 15, то есть три элемента:
• Первый и самый левый столбец содержит значения, большие или равные 0 и меньшие 5.
• Второй контейнер содержит значения, большие или равные 5 и меньшие 10.
• Третий и самый правый контейнер содержит значения, большие или равные 10 и меньшие или равные 15.
Сам код:
#Гистограммы
hist, bin_edges = np.histogram(x, bins=10)
fig, ax = plt.subplots()
ax.hist(x, bin_edges, cumulative=False)
ax.set_xlabel('x')
ax.set_ylabel('Frequency')
plt.show()
Функция np.histogram() — это удобный способ получить данные для гистограмм. Он берет массив с вашими данными и количеством (или ребрами) бинов и возвращает два массива NumPy:
• hist содержит частоту или количество элементов, соответствующих каждому бину.
• bin_edges содержит ребра или границы корзины.
Что рассчитывает histogram(), граф .hist() может показать графически. Первый аргумент .hist() — это последовательность с вашими данными. Второй аргумент определяет края бинов. Третий отключает возможность создания гистограммы с накопленными значениями. Результат представлен внизу:
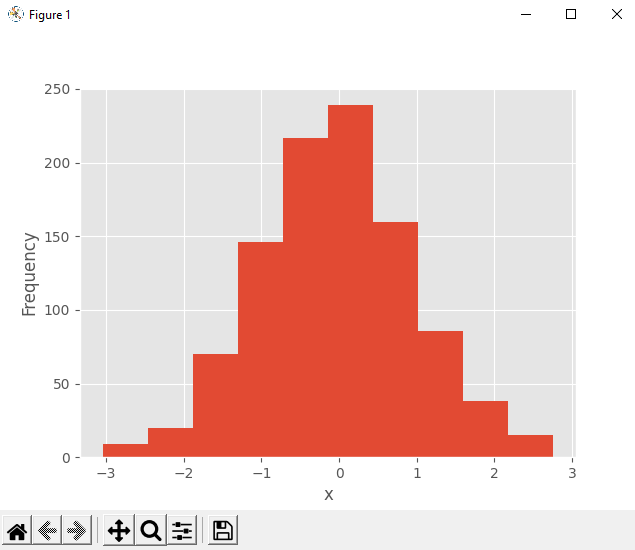
Вы можете видеть края корзины на горизонтальной оси и частоты на вертикальной оси.
При значении аргумента cumulative = True в .hist() можно получить гистограмму с совокупным количеством элементов:
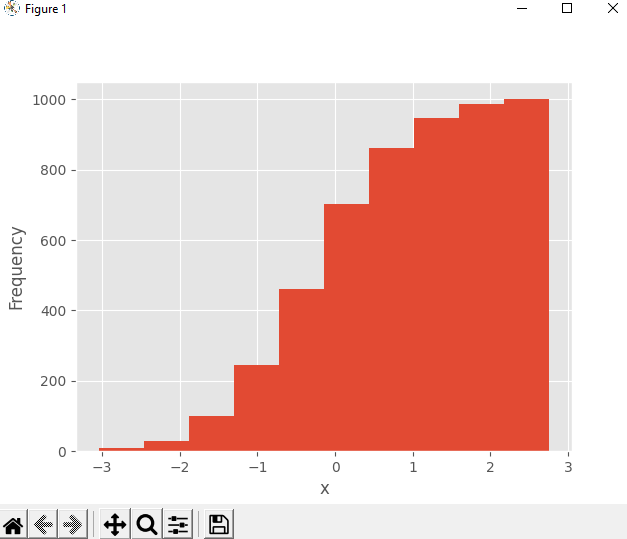
Частота первого и самого левого лотка — это количество элементов в этом лотке. Частота второго бина — это сумма количества элементов в первом и втором бинах. Другие контейнеры отрисовываются аналогично. Наконец, частота последнего и самого правого бина — это общее количество элементов в наборе данных (в данном случае 1000).
Pie Charts круговые диаграммы
Круговые диаграммы представляют данные с небольшим количеством меток и заданными относительными частотами. Они хорошо работают даже с ярлыками, которые нельзя заказать (например, номинальные данные). Круговая диаграмма представляет собой круг, разделенный на несколько частей. Каждый срез соответствует отдельной метке из набора данных и имеет площадь, пропорциональную относительной частоте, связанной с этой меткой. Сам код:
#Pie Charts круговые диаграммы
x, y, z = 128, 256, 1024
fig, ax = plt.subplots()
ax.pie((x, y, z), labels=('x', 'y', 'z'), autopct='%1.1f%%')
plt.show()
Первым делом мы определяем данные, связанные с тремя метками. Далее, Первый аргумент .pie() — данные, а второй — последовательность соответствующих меток. autopct определяет формат относительных частот, показанных на рисунке. Результат:
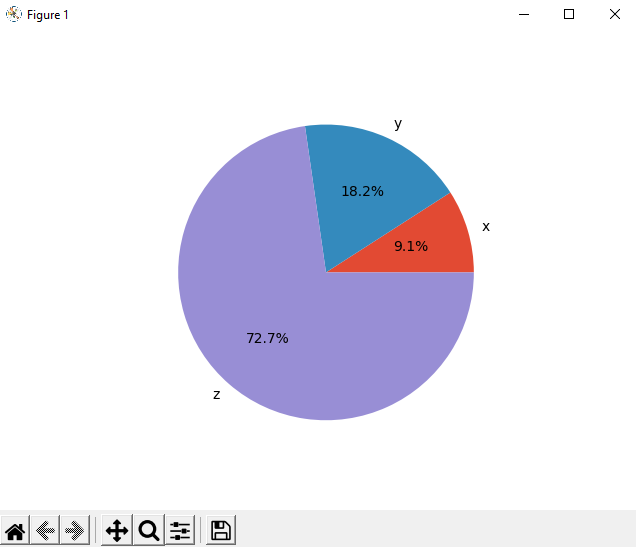
Круговая диаграмма показывает x как наименьшую часть круга, y как следующую наибольшую, а затем z как самую большую часть. Проценты обозначают относительный размер каждого значения по сравнению с их суммой.
Bar Charts
Гистограммы также иллюстрируют данные, которые соответствуют заданным меткам или дискретным числовым значениям. Они могут показывать пары данных из двух наборов данных. Элементы одного набора - это метки, а соответствующие элементы другого - их частоты. При желании они также могут отображать ошибки, связанные с частотами. Гистограмма показывает параллельные прямоугольники, называемые барами. Каждая полоса соответствует одной метке и имеет высоту, пропорциональную частоте или относительной частоте ее метки. Сам код:
#Bar Charts
x = np.arange(21)
y = np.random.randint(21, size=21)
err = np.random.randn(21)
fig, ax = plt.subplots()
ax.bar(x, y, yerr=err)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
В данном коде мы использовали np.arange(), чтобы получить x или массив последовательных целых чисел от 0 до 20. Мы использовали это для представления меток. y — это массив равномерно распределенных случайных целых чисел, также от 0 до 20. Этот массив будет представлять частоты. err содержит нормально распределенные числа с плавающей точкой, которые являются ошибками. Эти значения не являются обязательными. Далее создаем гистограмму с помощью .bar(), если вам нужны вертикальные столбцы или .barh(), если вам нужны горизонтальные столбцы. Результат:
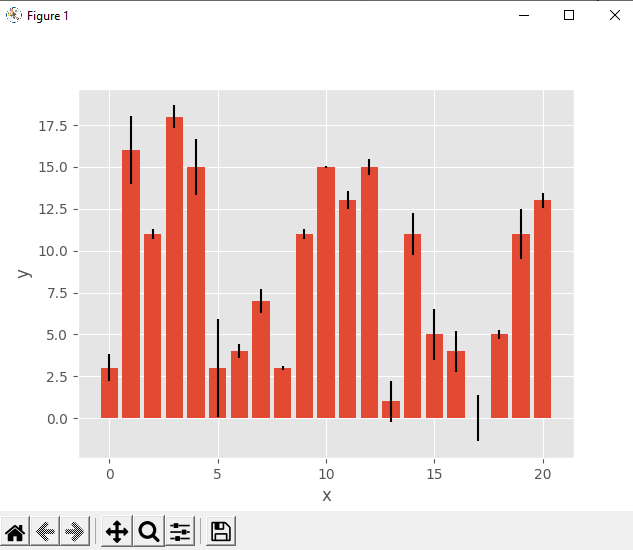
X-Y участки
Диаграмма x-y или диаграмма рассеяния представляет пары данных из двух наборов данных. Горизонтальная ось x показывает значения из набора x, а вертикальная ось y показывает соответствующие значения из набора y. При желании вы можете включить линию регрессии и коэффициент корреляции. Код построения представлен внизу:
#X-Y участки
x = np.arange(21)
y = 5 + 2 * x + 2 * np.random.randn(21)
slope, intercept, r, *__ = scipy.stats.linregress(x, y)
line = f'Regression line: y={intercept:.2f}+{slope:.2f}x, r={r:.2f}'
fig, ax = plt.subplots()
ax.plot(x, y, linewidth=0, marker='s', label='Data points')
ax.plot(x, intercept + slope * x, label=line)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(facecolor='white')
plt.show()
Сначала мы генерируем два набора данных и выполняем линейную регрессию с помощью scipy.stats.linregress().Набор данных x снова является массивом с целыми числами от 0 до 20. y вычисляется как линейная функция x, искаженная некоторым случайным шумом. linregress возвращает несколько значений. Вам понадобится наклон и точка пересечения линии регрессии, а также коэффициент корреляции r. Затем применяем .plot(), чтобы получить график x-y. Результат:

Схемы Зоны активности
Тепловая карта может быть использована для визуального отображения матрицы. Цвета представляют числа или элементы матрицы. Тепловые карты особенно полезны для иллюстрации ковариационных и корреляционных матриц. Вы можете создать тепловую карту для ковариационной матрицы с помощью .imshow():
#Схемы Зоны активности
matrix = np.cov(x, y).round(decimals=2)
fig, ax = plt.subplots()
ax.imshow(matrix)
ax.grid(False)
ax.xaxis.set(ticks=(0, 1), ticklabels=('x', 'y'))
ax.yaxis.set(ticks=(0, 1), ticklabels=('x', 'y'))
ax.set_ylim(1.5, -0.5)
for i in range(2):
for j in range(2):
ax.text(j, i, matrix[i, j], ha='center', va='center', color='w')
plt.show()
Здесь тепловая карта содержит метки «x» и «y», а также числа из ковариационной матрицы. Результат:
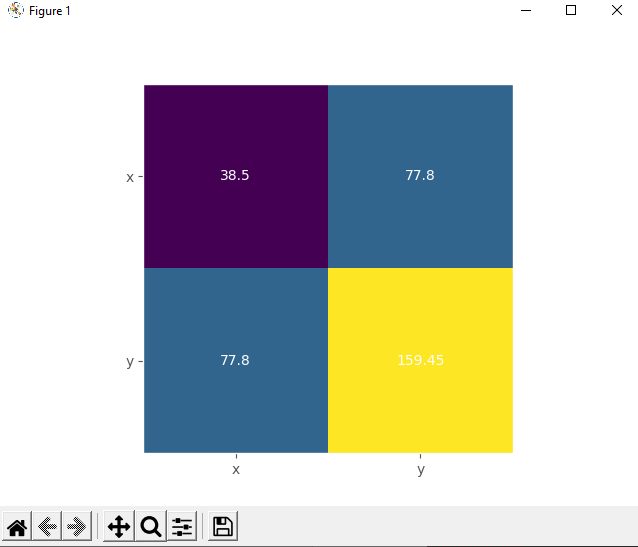
Желтое поле представляет самый большой элемент из матрицы 130.34, а фиолетовое соответствует наименьшему элементу 38.5. Синие квадраты между ними связаны со значением 77,8.
Вывод
Теперь, когда мы разобрали описательную статистику, вы можете смело применять ее на практике, причем реализовывая ее как на чистом Python, так и используя методы и функции библиотек, созданных специально для этих целей.

